Das Marktdiagramm

1.2.1.1 Das Angebot

Die Nachfrage

Zur Ermittlung des Angebots befragt der Verband der Dingerindustrie regelmäßig die Mitgliedsunternehmen. Da alle Unternehmen organisiert sind, ergibt sich ein vollständiges Bild. Die entscheidende Frage lautet, wie hoch die Stückkosten für Dinger sind. In den Mitgliedsunternehmen weiß man diesen Begriff zu interpretieren:

Abbildung 1

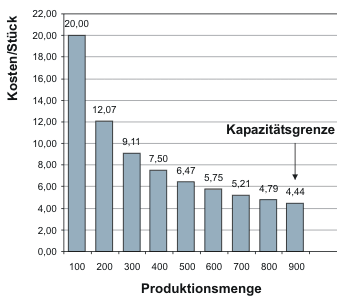
Aus früheren umfangreicheren Erhebungen ist bekannt, dass die Stückkosten in den einzelnen Unternehmen mit steigender Produktionsmenge sinken.* Für ein Unternehmen, das im Hinblick auf den typischen Kostenverlauf repräsentativ für die Unternehmen der Dingerindustrie ist, wurde folgender Kostenverlauf ermittelt:

Die geringsten Kosten pro Stück werden an der Kapazitätsgrenze erreicht. Bei einem gegebenen Verkaufspreis ist das Unternehmen daher natürlich an der Auslastung der Kapazität interessiert. Würden sich Dinger zurzeit für 9,75 € verkaufen lassen, könnte das Unternehmen seine Kosten nur decken, wenn es 300 oder mehr Stück pro Periode produzieren und absetzen würde. (Aufgrund der getroffenen Annahmen kann das Unternehmen seine Produktion zum herrschenden Preis immer absetzen. Es findet zum Marktpreis immer Abnehmer, sieht sich also nicht dem Problem fehlender Nachfrage gegenüber.) Bei jedem Preis über 4,44 € würde sich die Produktion von Dingern im betrachteten Unternehmen lohnen, da man in der Lage ist, zu Stückkosten von 4,44 € zu produzieren.

Da man im Verband weiß, dass die Unternehmen aufgrund des Stückkostenverlaufs die Kapazitäten grundsätzlich auslasten, wird nur nach der Höhe der Stückkosten bei einer Produktion von 900 Stück gefragt. Wir gehen davon aus, dass die Unternehmen ehrlich antworten.

Insgesamt gehören 348 Unternehmen dem Verband an. Dem Verband gehören auch Unternehmen an, die aktuell keine Dinger produzieren. Bei ihren Angaben zu den Stückkosten handelt es sich um Schätzungen.* Wegen der hohen Zahl der Unternehmen ist es notwendig, die Ergebnisse tabellarisch zusammenzufassen, um einen schnellen Überblick zu gewinnen. Die nachstehende Tabelle zeigt die Zahl der Unternehmen mit Stückkosten in den jeweils angegeben Bereichen:

Man sieht, dass es zwei Unternehmen gibt, die über eine sehr effiziente Technologie verfügen, da sie in der Lage sind, Dinger zu Stückkosten unter 4 € herzustellen. Der Modus (häufigste Wert) liegt bei Stückkosten von 4,75 €.

Aus einer anderen Markterhebung ist bekannt, dass der Marktpreis für Dinger in der letzten Periode bei 7,00 € lag und 255,6 Tausend Dinger verkauft werden konnten. Ist diese Information mit der Stückkostenerhebung kompatibel?

Unternehmen, die Dinger nur zu Stückkosten über 7,00 € herstellen konnten, hatten kein Interesse, Dinger zum herrschenden Marktpreis herzustellen, da sie ja offensichtlich mit jedem Ding Verlust gemacht hätten. Also kommen als Anbieter nur Dinger-Produzenten mit Stückkosten unter 7,00 € in Frage. Sie haben auch ein Interesse, Dinger zu verkaufen, denn sie machen ja mit jedem verkauften Ding Gewinn . Tabelle 1 lässt sich entnehmen, dass dies auf 284 Unternehmen zutrifft. Da jedes Unternehmen 900 Stück produziert, ergibt sich eine Gesamtproduktion von 255.600 Stück. Die Ergebnisse der beiden Erhebungen passen also exakt zusammen.

Wenn wir diese Überlegung für alternative Marktpreise wiederholen, gewinnen wir die Information, für wie viele Unternehmen sich das Angebot in Gewinn auszahlt und wie viele Dinger angeboten werden. Diese Information fassen wir zusammen und übertragen sie in das Marktdiagramm.

Natürlich finden wir in der Tabelle (wie im Marktdiagramm) die Information wieder, dass (von 284 Unternehmen) bei einem Preis von 7,00 € ein Angebot von insgesamt 255.600 Stück geplant wird. Würde der Preis auf 4,00 € sinken, würde sich die Produktion nur noch für die beiden effizientesten Unternehmen lohnen und das Angebot auf 1800 Stück sinken.

Abbildung 2

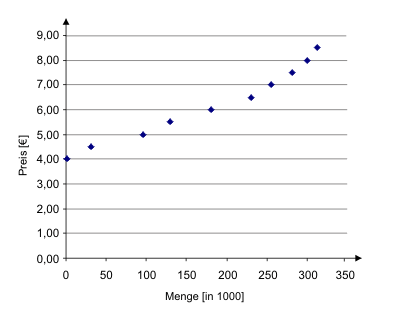
Eine Angebotsfunktion (oder -kurve) konstruieren wir nun durch die Verbindung der Punkte. Dass sich dabei eine stufige (unstetige) Funktion mit großen Sprüngen ergibt, ist auf die Zusammenfassung der Befragungsergebnisse in Klassen zurückzuführen.

Abbildung 3

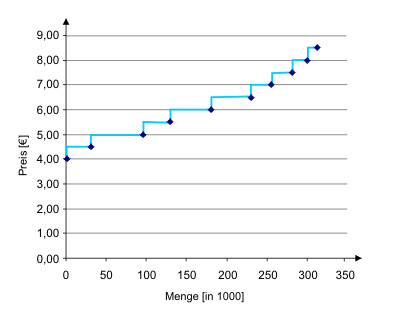
Hätten wir mehr Klassen gebildet, hätten wir einen "glatteren" Verlauf erhalten. Vollkommen glatt wird die Angebotsfunktion in diesem Beispiel natürlich nicht verlaufen, da die Produktionsentscheidung jedes einzelnen Unternehmens nur 900 oder 0 Stück sein kann. Deswegen weist die Angebotsfunktion waagerechte Teilbereiche auf, die mindestens einer Breite von 900 Stück entsprechen, auch wenn wir jedes Unternehmen einzeln erfassen. Da 900 Stück bezogen auf das gesamte Volumen, das bei einem Preis von 7,00 € ja über 255 Tausend Stück ausmachen würde, im Diagramm einer so kurzen Strecke entsprechen, die optisch kaum auszumachen wäre, zeichnen wir die Angebotsfunktion als stetige Funktion. Mit einer Lupe könnten wir aber erkennen, dass die einzelnen Punkte, aus denen sich die Angebotsfunktion zusammensetzt, 900 Einheiten auseinander liegen.

Abbildung 4

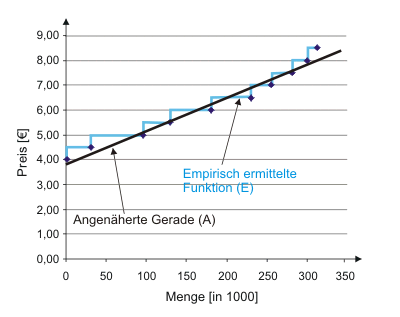
Da sich die gefundene Angebotsfunktion recht gut durch eine Gerade annähern lässt, wollen wir auch diesen Schritt der Vereinfachung noch durchführen. Zwar entspricht diese Angebotsfunktion unseren Daten nur noch ungefähr, aber wir nehmen die Abweichungen in Kauf. Schließlich gewinnen wir eine Funktion, mit der wir sehr einfach umgehen können.

Nun können wir die Angebotsfunktion verwenden, um das geplante Angebot der Dinger-Produzenten schnell und einfach zu ermitteln. Abbildung 5 zeigt, wie wir vorzugehen hätten, um in Erfahrung zu bringen, welches Angebot die Produzenten planen würden, wenn sie damit rechneten, Dinger zum Preis von 6 € verkaufen zu können. Aus der Grafik lesen wir dem grünen Pfeil folgend ab, dass eine Produktion von etwa 165.000 Dinger geplant würde. Zum Vergleich ist dargestellt, welche Information sich mit der unstetigen Angebotskurve (180.000 Stück; s. Tabelle) ergeben hätte.

Abbildung 5

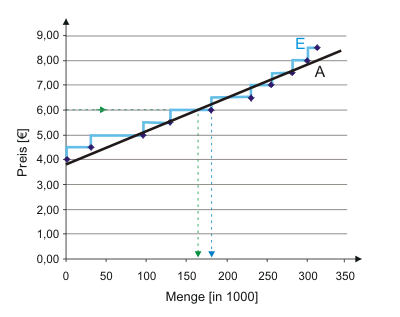
Die Angebotsfunktion kann man nicht in der entgegengesetzten Richtung interpretieren: "Wenn 165.000 Dinger hergestellt werden, beträgt der Preis 6 €." Diese Aussage ist nicht zulässig. Dass sie wenig Sinn macht, erkennt man auch daran, dass die Angebotsfunktion dann ja anzeigen würde, dass der Dingerpreis mit zunehmender Produktion anstiege. Je mehr hergestellt wird, desto höher der Preis? Das widerspricht jeder Erfahrung.

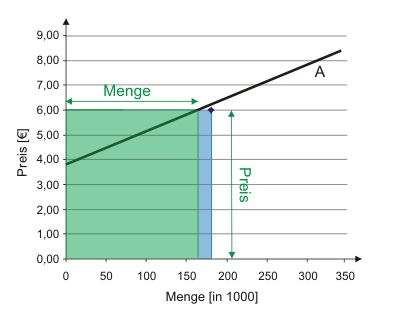
Da wir jetzt zu alternativen Preisen die jeweiligen Angebotsplanungen der Produzenten ablesen können, ist es nur ein kleiner Schritt, aus dem Diagramm die Umsatzerwartung zu bestimmen. Der erwartete Umsatz entspricht dem erwarteten Preis multipliziert mit der geplanten Angebotsmenge. Kurz: Umsatz = Preis mal Menge. Im Diagramm entspricht die Höhe des grün schraffierten Rechtecks dem erwarteten Preis, die Breite entspricht der geplanten Produktionsmenge. Wenn wir die Höhe mit der Breite multiplizieren, erhalten wir die Fläche. Sie entspricht also dem erwarteten Umsatz.

Vielleicht ist Ihnen aufgefallen, dass hier konsequent von erwarteten Größen die Rede ist: die Unternehmen erwarten Preise, sie erwarten Kosten, sie planen die Produktion. In der Folge werden wir etwas nachlässiger mit den Begriffen umgehen und nicht jedes Mal ausdrücklich erwähnen, dass es sich um erwartete oder geplante Größen handelt. Dennoch sollte immer bedacht werden, dass wir hier die Pläne untersuchen, die die Wirtschaftssubjekte aufstellen. Wir haben im Moment noch keinen Hinweis darauf, welcher Preis sich am Markt herausbilden wird. Inzwischen wissen wir aber für jeden Preis, welche Menge die Unternehmen anzubieten wünschen.

Abbildung 6

Jetzt fehlt uns eigentlich nur noch eine Prognose, wie die Unternehmen ihre Absatzpreiserwartungen bilden. Im Modell stellt dies kein Problem dar, denn wir gehen ja von vollkommener Information aus, die die Unternehmen in die Zukunft blicken lässt. Sie kennen also den Preis.

Tatsächlich könnten wir z. B. unterstellen, dass die Unternehmen immer den Preis für die Folgeperiode vermuten, der aktuell gültig ist ("statische Erwartungen"). Natürlich könnten wir auch kompliziertere Erwartungsbildungshypothesen unterstellen, wie etwa, dass die Unternehmen die Preisentwicklung in der Vergangenheit trendmäßig fortschreiben (also Zeitreihenanalyse betreiben). Aber egal wie die Hypothesen über die Absatzpreise zustande kommen, wir können mithilfe der Angebotsfunktion für jeden beliebigen Preis angeben, welche Unternehmen als Anbieter auftreten und wieviel sie insgesamt anbieten werden.

Gewinne und Kosten im Marktdiagramm

Eine simple Erklärung der "Produzentenrente"

Aus dem Angebotsdiagramm lassen sich neben den geplanten Produktionsmengen und erwarteten Umsätzen auch die erwarteten Kosten ablesen. Mit Umsätzen und Kosten ist dann natürlich auch der Gewinn bekannt, der als Differenz von Umsatz und Kosten definiert ist.

Bevor wir betrachten, wie wir den Gewinn herausfinden, sei darauf hingewiesen, dass wir an dieser Stelle noch nicht sauber zwischen lang- und kurzfristiger Betrachtung unterscheiden. Deswegen wollen wir hier zusätzlich davon ausgehen, dass die Unternehmen keine Fixkosten (s. Kosten) haben; das würde bedeuten, ihre Kosten wären gleich null, wenn sie die Produktion einstellen würden. In der Terminologie der Betriebswirtschaftslehre hieße das, dass Gewinn und Deckungsbeitrag übereinstimmen, denn es gilt:

Deckungsbeitrag = Umsatz - variable Kosten

und

Gewinn = Deckungsbeitrag - fixe Kosten.

Betrachten wir die 71 Unternehmen der Dingerindustrie, von denen uns bekannt ist (s. Tabelle 1), dass sie Stückkosten zwischen 4,51 und 5.00 € haben. Da wir nur diese zusammengefasste Information und nicht aus jedem Unternehmen die exakten Stückkosten kennen, gehen wir einfach davon aus, dass diese Unternehmen alle Stückkosten von 5.00 € haben. Damit machen wir einen kleinen Fehler, den wir aber in Kauf nehmen wollen.

Von diesen 71 Unternehmen wissen wir, dass sie - vorausgesetzt der Preis liegt höher als 5,00 € - jeweils 900 Dinger herstellen. Insgesamt stellen sie also 63900 (71 mal 900) Dinger her. Diese Menge wird als roter waagerechter Doppelpfeil im Diagramm angezeigt. Multiplizieren wir die Menge mit den Stückkosten, erhalten wir die rote Fläche, die nun die Produktionskosten aller 71 Unternehmen anzeigt.

Abbildung 1

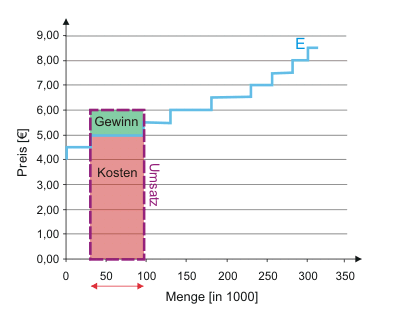
Wir nehmen nun als Beispiel an, die Unternehmen planen mit einem Dingerpreis von 6 €. Für alle Unternehmen, die zu diesem Preis kostendeckend anbieten können, wiederholen wir die Ermittlung der Kosten.

Abbildung 2

Abbildung 3

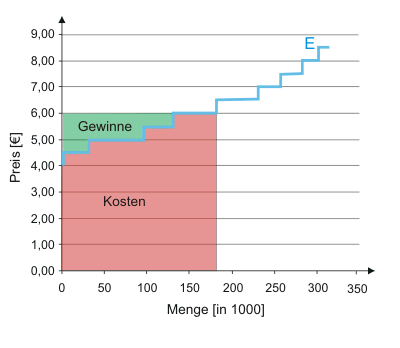
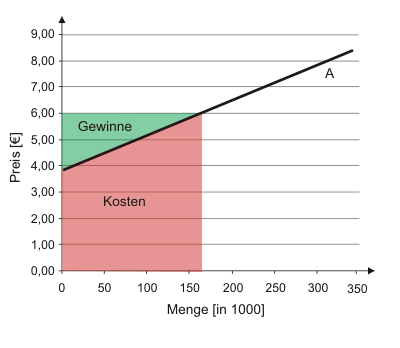
Da wir den Umsatz bereits kennen, können wir den erwarteten Gewinn als Differenz der Umsatz- und Kostenfläche im Diagramm ablesen. Die Unternehmen mit Stückkosten in Höhe von 6,00 €, die mit dem Absatzpreis übereinstimmen, erzielen keine Gewinne - sie machen aber auch keine Verluste. "Keine Gewinne erzielen" heißt allerdings nicht, dass die Unternehmer verhungern müssten. Ihre Leistung im Betrieb (Management, dispositive Arbeit) wird (kalkulatorisch) entlohnt und ihr Kapitaleinsatz marktüblich verzinst. Beides ist somit in den Stückkosten berücksichtigt. Würden diese Unternehmen allerdings mit einem geringeren Preis rechnen, dann würde sich die Produktion von Dingern nicht mehr lohnen. Die Umsätze reichten dann nicht mehr aus, die unternehmerische Leistung und/oder das eingesetzte Kapital marktüblich zu entlohnen. Für den Unternehmer wäre es vorteilhafter, seine Arbeitsleistung auf dem Arbeitsmarkt zu verkaufen und das Kapital zur Bank zu tragen. Die Unternehmen, die sich zum herrschenden Preis gerade so am Markt halten, werden mitunter Grenzanbieter genannt.

Natürlich werden wir auch hier in der Regel auf die lineare Angebotsfunktion zurückgreifen. Bei einem erwarteten Preis von 6 € würden sich Kosten und Gewinne wie folgt darstellen lassen.

Die grüne Fläche in Abbildung 3 wird uns später unter dem Namen Produzentenrente wieder begegnen.

|           | Impressum